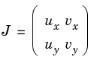There are special built-in operators available for modeling and for evaluating results; these operators are similar to functions but behave differently. Many physics interfaces use these operators to implement equations and special functionality. See Table 5-8 and the detailed descriptions that follow.
|
adj(expr)
|
||
|
Apply backward differentiation formula of order i on expression.
|
||
|
bndenv(expr)
|
Evaluates the expression expr at the coordinates of a particle or ray at a boundary.
|
|
|
centroid(expr)
|
Evaluates the expression expr in the centroid of the mesh element to which the point belongs.
|
|
|
circumcenter(expr)
|
Evaluates the expression expr in the circumcenter of the mesh element to which the point belongs.
|
|
|
dest(expr)
|
||
|
down(expr)
|
||
|
Tangential differentiation of an expression f defined on a boundary with respect to a spatial dimension x.
|
||
|
The square of the length of the global vector (exprx, expry, exprz) computed in the mesh element’s own metric.
|
||
|
env(expr)
|
Evaluates the expression expr at the coordinates of a particle or ray in a domain.
|
|
|
error(‘string’)
|
||
|
Functional sensitivity with respect to control variable p.
Functional sensitivity with respect to imaginary part of control variable p. |
||
|
isdefined(variable)
|
||
|
isinf(expr)
|
||
|
islinear(expr)
|
||
|
isnan(expr)
|
||
|
True if the derivative of the expression expr with respect to the solution depends on the solution or var, respectively.
|
||
|
mean(expr)
|
||
|
noenv(expr)
|
Evaluates an expression expr that is defined only on particles or rays, not the domain or boundary where the particles or rays are located.
|
|
|
nojac(expr)
|
||
|
Differentiation operator. Differentiation of f with respect to x. No chain rule for dependent variables.
|
||
|
Evaluate expression at the ith previous time step.
|
||
|
residual(expr)
|
||
|
Evaluates the expression expr at an i-dimensional entity in the point with coordinates given by the coordinate expressions coordinate exprs.
|
||
|
Define temporary constant in withsol.
|
||
|
shapeorder(variable)
|
||
|
side(entity,expr)
|
||
|
test(expr)
|
||
|
timeint, timeavg
|
||
|
timemax, timemin
|
||
|
treatasconst(expr)
|
Treat expr as independent of the solution.
|
|
|
Evaluate the flux associated to a dependent variable u into the domains on the up and down sides of a boundary, respectively.
|
||
|
up(expr)
|
||
|
var(expr,fieldname1, fieldname2, ...)
|
||
|
•
|
When you apply the adjoint sensitivity operator adj to an expression, COMSOL uses the adjoint sensitivity solution instead of the primal solution for the evaluation.
|
|
•
|
The at operator can access a solution to a time-dependent problem at any time. COMSOL provides the solution at that time using interpolation. You can use the at operator to compare two solutions at different times during results evaluation; for example, at(30,u)-at(20,u) is the difference between the solution at 30 s and the solution at 20 s.
|
|
•
|
The first input argument is the time. The second input argument is the expression that you want to evaluate using this solution. For example, at(12.5,u) is the solution at 12.5 s. The time must be within the simulation time span but does not have to be a specified output time. If it is not, then the at operator uses interpolation to compute the data values at that time.
|
|
•
|
You can also use 'first' or 'last' as the first argument to evaluate an expression at the first or last time of the simulation, respectively.
|
|
•
|
The at operator can only be used during results evaluation, so it should not be used when setting up the model.
|
|
•
|
The atlocal operator takes 2, 3, or 4 arguments depending on the dimension of the geometrical entity it is being evaluated on.
|
|
•
|
For example, on a three-dimensional entity, atlocal(xi1,xi2,xi3,expr) evaluates expr at the point with local coordinates (ξ1, ξ2, ξ3) in each mesh element. On a two-dimensional entity the syntax is atlocal(xi1,xi2,expr) and on a one-dimensional entity it is atlocal(xi1,expr).
|
|
•
|
The attimemax and attimemin operators evaluate an expression at the time where another expression achieves its maximum or minimum, respectively. attimemax(t1,t2,expr1,expr2) finds the time t0 on the interval t1 ≤ t ≤ t2 where expr1(t) is maximal and computes expr2(t0). The first two arguments must be real constants.
|
|
•
|
attimemax(t1,t2,expr1,expr2,'nointerp') and attimemin(t1,t2,expr1,expr2,'nointerp') evaluate the maximum or minimum without doing any interpolation between the stored time steps. This variant might be less accurate but faster and more robust.
|
|
•
|
The attimemax and attimemin operators can only be used during results evaluation, so you cannot use then when setting up the model. See timemax and timemin for similar operators.
|
When working with extra dimensions, evaluation can be done in either a standard base geometry, in an extra dimension geometry, or a product of a base geometry and one or several extra dimension geometries. The atxd, atonly, and noxd operators modify the evaluation context by adding or removing geometries from the current product.
All of these operators have a scope indicating the base geometry or extra dimension to which they belong. The scope for base geometries is typically comp1, comp2, and son on, while the scope for extra dimensions is typically xdim1, xdim2, and so on. Also, the atxd operators have a suffix 0, 1, 2, or 3, which indicates the dimension of the geometric entities where their argument is evaluated. So, the complete name of an atxd operator is, for example, xdim1.atxd2, and the complete name of an atonly or noxd operator is, for example, comp1.atonly or xdim1.noxd.
The atxd operators add another geometry to the current product. Suppose, for example, that you have a 2D base geometry with scope comp1, and a 2D extra dimension geometry with scope xdim1. Starting in an evaluation context in the base geometry, xdim1.atxd1(2,3,expr) evaluates expr in the product of comp1 and xdim1, at a point on the boundary in xdim1 with coordinates (2, 3). Starting in an evaluation context in the extra dimension, comp1.atxd2(4,5,expr) evaluates expr in the product of comp1 and xdim1, at a point in a domain in comp1 with coordinates (4, 5).
When there is a product of a base geometry with more than one extra dimension, several nested atxd operators can be used to specify evaluation in the product. For example, suppose xdim2 and xdim3 are 1D extra dimensions attached to a base geometry comp1. Starting in the base geometry, xdim2.atxd1(2,xdim3.atxd0(3,expr)) evaluates expr in the product of comp1 with xdim2 and xdim3. The order of applying the two operators is inconsequential.
The following points are worth noting about the atxd operators:
|
•
|
The number of arguments is always sdim+1, where sdim is the dimension of the geometry indicated by the scope of the operator.
|
|
•
|
The first sdim arguments specify coordinates in this geometry. They must be constant in the current evaluation context.
|
|
•
|
The atonly operators remove all but one geometries from the current product. Consider again the example where comp1 is a base geometry and xdim1 is an extra dimension. Starting in the product of comp1 and xdim1, comp1.atonly(expr) evaluates expr in the base geometry, and xdim1.atonly(expr) evaluates expr in the extra dimension.
The noxd operators are similar to the atonly operators, but instead remove a single geometry from the current product. This is most useful in products with more than one extra dimension, because in products with just one extra dimension, an atonly operator can be used instead. For example, in the product of a base geometry comp1, and extra dimensions xdim2 and xdim3, xdim2.noxd(expr) evaluates expr in the product of comp1 and xdim3.
|
•
|
The ballint(r, expr) operator computes the volume integral of the expression expr in a ball with radius r around the point in which it is evaluated. The ballint operator can be evaluated on all entities in 3D.
|
|
•
|
|
•
|
The circint(r, expr) operator computes the curve integral of the expression expr on a circle with radius r around the point in which it is evaluated. The circint operator can be evaluated on all entities in 2D and on edges in 3D, when used in 3D the integration is done on the circle in the normal plane to the edge.
|
|
•
|
|
•
|
The diskint(r, expr) is similar to the circint operator but calculates the surface integral on a disk instead.
|
|
•
|
|
•
|
The sphint(r, expr) is similar to the ballint operator but computes the surface integral on a sphere instead.
|
|
•
|
|
•
|
All of operators can be used with a third argument N that approximately specifies the number of integration points used — for example, circint(r, expr,100).
|
|
•
|
To all operators you can add a suffix (“_frameId”) that specifies the frame in which the integration is done — for example, circint_spatial(r, expr).
|
|
•
|
The expression expr may contain the dest operator. The dest operator forces its expression to be evaluated in the center of the sphere or circle. You can use it, for instance, with a sphint operator to write expressions including the sphere’s normal direction.
|
|
•
|
Use the bdf operator to approximate time derivatives when the time discrete solver is used.
|
|
•
|
The expression bdf(expr, i) results in a discretization of the time derivative of expr using a backward differentiation formula.
|
|
•
|
The second argument, i, determines the order of accuracy of the discretization. Currently, first order and second order is available, so allowed values are i = 1 and i = 2. A second-order formula requires access to two previous time steps. Because this is not possible at the initial step, the evaluation at the initial step always uses the first-order formula.
|
|
•
|
The bdf operator can be implemented using the prev operator. For example, obtain the first-order backward differentiation formula, also known as the backward Euler method, through bdf(u,1) = (u-prev(u,1))/timestep.
|
|
•
|
If you have selected Compute boundary fluxes in a physics interface defining a dependent variable u, uflux(u) and dflux(u), when evaluated on a boundary, give an accurate value of the boundary flux into the domains on the up and down side of the boundary, respectively.
|
|
•
|
If you have not selected Compute boundary fluxes, the uflux and dflux operators give a less accurate value of the flux into the domain, based on the gradient of u. The less accurate method is always used if the operators are evaluated during solution because accurate boundary fluxes are not available then.
|
|
•
|
The flux for different frames can be obtained by appending _material, _spatial, _mesh, or _geometry to the operator names. The default is the material frame.
|
 |
The uflux and dflux operators are only applicable to dependent variables defined by physics interfaces that support accurate boundary fluxes.
|
|
•
|
The centroid(expr) operator evaluates the expression expr in the centroid of the mesh element to which the point belongs.
|
|
•
|
The circumcenter(expr) operator evaluates the expression expr in the circumcenter of the mesh element to which the point belongs. This point is in general only well defined for simplices. For other mesh elements, a point with approximately the same distance to all vertices of the mesh element is computed.
|
|
•
|
You can add a suffix (“_frameId”) that specifies the frame in which the evaluation is done — for example, circumcenter_spatial(expr).
|
|
•
|
All differentiation operators (d, pd, and dtang) can be used both in model settings and in results evaluation.
|
|
•
|
Use the d operator to differentiate a variable with respect to another variable, using the chain rule for dependent variables. For example, d(T,x) means differentiation of T with respect to x. Some space derivatives are also available using predefined variables. For example, uxx, d(ux,x), and d(d(u,x),x) are equivalent for a dependent variable u when evaluated in a domain. On a boundary, however, d(u,x) is 0, while ux is the average of the values from the adjacent domains.
|
|
•
|
The pd operator works in a similar way to the d operator. The main difference is that pd(u,x) is 0 rather than ux (no chain rule is applied for dependent variables).
|
|
•
|
Use the dtang operator to compute derivatives in the tangential direction along a boundary. The dtang operator can be applied to expressions that are only defined on the boundary and therefore cannot be differentiated by the d operator. In a 3D model, (dtang(f,x), dtang(f,y), dtang(f,z)) is a vector in the tangent plane of a boundary at the point where it is evaluated, and similarly in a 2D model, (dtang(f,x), dtang(f,y)) is a vector in the tangent line of a boundary point. When evaluated in a domain, dtang(f,x) is the same as d(f,x). The second argument of dtang(f,x) must be one of the spatial coordinates. Not all quantities have rules for evaluating tangential derivatives. Applying dtang(f,x) to an expression with no tangential derivative rule results in an error message.
|
|
•
|
Time derivatives can be written as d(u,t) or d(u,TIME) depending on the context. If the model does not contain any ALE (arbitrary Lagrangian-Eulerian) formulation, always use d(u,t) (or ut). In the presence of ALE, d(u,TIME) computes the time derivative for fixed points in the mesh and is usually the best way to compute a time derivative because d(u,t) is not supported for many variables.
|
The expressions d(u^2,u) and pd(u^2,u) both equal 2*u; d also takes the spatial and time variables into account and treats their derivatives accordingly. In other words, if u is the dependent variable and x and t are the spatial coordinate and time, respectively, then d(u+x,x) equals ux+1 (ux is the spatial derivative of u with respect to x), while pd(u+x,x) equals 1 because u is considered to be independent of anything but itself in the case of pd. Equivalently, d(u,t) equals ut, while pd(u,t) is zero.
If a time-dependent model contains two dependent variables u and v, use d(u*v,t) to compute the derivative of the product uv with respect to time t. The d operator uses the chain rule and is equivalent to u*vt+ut*v (using COMSOL syntax). pd(u*v,t), on the other hand, is zero.
If u is a dependent variable defined only on a boundary, d(u,x) is not defined, but the tangential derivative dtang(u,x) can be evaluated on the boundary. The tangential derivative obeys most of the common differentiation rules, such as the product rule and the chain rule; however, dtang(x,x) is not always equal to 1.
|
•
|
The depends(expr) operator returns 1 if the expression expr that it operates on depends on the solution; otherwise it returns 0.
|
|
•
|
The dest (destination) operator is available for the following operators:
|
•
|
The dest operator forces the expression that it operates on to be evaluated on the destination points instead of the source points. This means that the destination operator can be used to create convolution integrals and other integral transforms. For instance, integrating the expression u/((dest(x)-x)^2+(dest(y)-y)^2) gives the following function of x and y:
The dest operator can also be used in the operator listed in the section ball, circle, disk, and sphere. In this context the forced point of evaluation is the center of the sphere or circle. You can use it, for instance, with a sphint operator to write expressions including the sphere’s normal direction.
The emetric(vector) returns the square of the length of a material 2-vector computed in the mesh element’s own metric. In this metric, the edges of the mesh element typically have length 1, and vectors orthogonal to the element have length 0. The number of input arguments defining the vector should be equal to the space dimension.
 |
|
•
|
Evaluating env(expr) on a particle or ray evaluates expr at the point in the domain where the particle or ray is. When evaluating a variable var on a particle or ray, if the variable is not defined on the particle or ray it is automatically replaced by env(var). Therefore the env operator can often be omitted.
|
|
•
|
Evaluating bndenv(expr) on a particle or ray, evaluates expr at the point on the boundary where the particle or ray is. If the particle or ray is not on a boundary, the evaluation fails. Use this operator instead of env when evaluating expressions that are only defined on boundaries.
|
|
•
|
The noenv(expr) operator can only be used as part of an expression within the env(expr) or bndenv(expr) operator. The noenv(expr) operator is used to evaluate an expression expr that is defined for particles or rays but is not defined at their locations within a domain or on a boundary. For example, if you write env(expr1*noenv(expr2)), then the expr1 must be defined in the domain where the particle or ray is, and expr2 must be a quantity that is defined for individual particles or rays, such as the particle speed.
|
|
•
|
|
•
|
You can for instance use this operator to make assertions on how your solution should behave. If you write if(cond,expr,error(’cond is false’)) expr is calculated when cond is true and an error message is generated including the text cond is false, when cond is false.
|
|
•
|
The functional sensitivity operator fsens evaluates the sensitivity of the current objective functional with respect to the control variable given as the single argument. Note that the argument must be a control variable name; other dependent variables or general expression are not allowed.
|
|
•
|
The functional sensitivity operator fsensimag evaluates the sensitivity of the current objective functional with respect to the imaginary part of the control variable given as the single argument.
|
|
•
|
|
•
|
The first argument is a condition that COMSOL treats as a Boolean expression. If — at a particular evaluation point — cond is true, then the second argument is evaluated, otherwise the third argument is evaluated. That is, only one branch is evaluated at any evaluation point.
|
|
•
|
Use the if operator to avoid illegal operations. For example, if(x==0,1,sin(x)/x) is a valid and continuous expression for all values of x, including x = 0.
|
|
•
|
integrate(expr,var,lower,upper) computes the integral of expr for the integration variable var over an interval specified by expressions lower for the lower limit and upper for the upper limit. The expressions for lower and upper limits do not have to be constants but are required to evaluate to real values.
|
|
•
|
integrate(expr,var,lower,upper,tol) sets the relative tolerance in the numerical integration to tol. The default value of the relative tolerance (used when the fifth argument is omitted) is 1e-3. The tolerance must be a real constant between 0 and 1.
|
|
•
|
It is possible to use a coordinate name as the integration variable in the integrate operator. Note, however, that this will not change the evaluation point where the first argument is evaluated. For example, if u is a dependent variable, integrate(u,x,a,b) is equivalent to u*integrate(1,x,a,b).
|
|
•
|
To evaluate an integral over a geometrical curve, the integrate operator can be combined with one of the spatial at operators. For example, in a 2D model, integrate(comp1.at2(x,y,u),x,a,b) will integrate u along the line segment with end points (a, y) and (b, y).
|
|
•
|
The isinf operator returns 1 if the expression that it operates on evaluates to infinity (or minus infinity); otherwise it returns 0.
|
|
•
|
The isnan operator returns 1 if the expression that it operates on evaluates to NaN (not-a-number); otherwise it returns 0.
|
|
•
|
The islinear operator returns 1 if the expression that it operates on is a linear function of the solution; otherwise it returns 0.
|
|
•
|
The jacdepends(expr) operator returns 1 if the derivative of the expression expr, with respect to any part of the solution, depends on the solution; otherwise it returns 0.
|
|
•
|
jacdepends(expr, var) returns 1 if the derivative of the expression expr, with respect to any part of the solution, depends on var; otherwise it returns 0.
|
The lindev operator evaluates its argument in the following way when the solution has a stored linearization point: The expression is first linearized at the linearization point and then evaluated at the current solution. In particular, if f depends linearly on the solution, lindev(f) is the same as f. If f does not depend on the solution, lindev(f) is 0. If the solution does not have a stored linearization point, using lindev causes an error message.
The linper operator has one single use: To indicate load terms that should be used by stationary solvers setting Linearity to Linear perturbation in the Settings window for Stationary Solver. Terms not enclosed by linper are ignored by such solvers. On the other hand, terms inside linper are ignored by all other solvers.
The linpoint operator can access the linearization point in a solution with a stored linearization point. If the solution does not have a stored linearization point, using linpoint causes an error message.
The linsol operator evaluates an expression using the standard solution. This is the default, so in most contexts the operator is not very useful. However, it can, for example, be used inside the argument of linpoint to evaluate a part of the expression with the standard solution instead of the linearization point.
The lintotal operator can access the sum of the linearization point and the linear perturbation in a solution with a stored linearization point. If the solution does not have a stored linearization point, using lintotal causes an error message.
The lintotalavg operator evaluates the average of an expression over all phases. lintotalavg(f) is evaluated by taking the average of lintotal(f) with the solution (but not the linearization point) multiplied by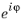 
for a number of phases 
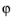. The number of phases is automatically selected to achieve an accurate value. lintotalavg(f,n) uses n equidistantly spaced phases.
for a number of phases . The number of phases is automatically selected to achieve an accurate value. lintotalavg(f,n) uses n equidistantly spaced phases.The lintotalpeak operator evaluates the maximum of an expression over all phases. lintotalpeak(f) is evaluated by taking the maximum of real(lintotal(f)) with the solution (but not the linearization point) multiplied by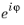 
for a number of phases 
. The number of phases is automatically selected to achieve an accurate value. lintotalpeak(f,n) uses n equidistantly spaced phases.
for a number of phases 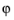. The number of phases is automatically selected to achieve an accurate value. lintotalpeak(f,n) uses n equidistantly spaced phases.The lintotalrms operator evaluates the RMS of an expression over all phases. lintotalrms(f) is the same as sqrt(lintotalavg(abs(f)^2)).
The linzero operator evaluates an expression using a zero solution. This is mostly used internally in the definitions of some other operators.
|
•
|
The mean operator can be called on any entity that has a lower dimension than the model. The dimension of the entity from where the call is made is called n.
|
|
•
|
The mean operator determines the smallest integer m>n for which there are adjacent entities of dimension m. It then evaluates the expression at the point one time for each m dimensional adjacent entity, regarding the point as a point in the entity, and takes the average of the calculated values.
|
|
•
|
The nojac operator makes sure that any expression that it operates on is excluded from the Jacobian computation (it prevents all symbolic differentiation). This is useful if a Jacobian contribution is not strictly necessary and the computational requirements for it are high, such as when using a nonlocal coupling. The use of the nojac operator can then significantly lower the memory requirements by avoiding fill-in of the Jacobian matrix, but its use might also slow down the convergence of the solution.
|
|
•
|
The k-ε turbulence model is an example where a built-in use of the nojac operator improves performance.
|
|
•
|
When the ppr operator is applied on an expression, the COMSOL Multiphysics software uses polynomial-preserving recovery to evaluate all variables in the expression that are discretized using Lagrange shape functions. For example, if e = ux + vy, then ppr(e^2)=(ppr(ux)+ppr(vy))^2. For other shape function types, the operator has no effect.
|
 |
|
•
|
The pprint operator similarly applies polynomial-preserving recovery within each group of domains with equal settings. Use these operators to get an estimate of the discretization error in the gradient. For example, ux-pprint(ux) in a 1D model.
|
 |
|
•
|
The expression prev(expr, i) evaluates expr using the solution obtained i time steps before the current time step.
|
|
•
|
When used in equations, the prev operator makes it possible to discretize time derivatives. For example, to discretize ut (the time derivative of u) with the formula known as the backward Euler method, use the expression (u-prev(u,1))/timestep. Here, timestep is the size of the time step used to reach the current solution u. The prev operator is also applicable for timestep. For example, prev(timestep,1) is the size of the time step used to reach the solution at the previous time step.
|
|
•
|
When using the prev operator, sufficiently many previous time steps must be stored. Specify the number of previous time steps to store in the time discrete solver (time discrete levels) in the Number of time discrete levels field in the General section of the Settings window for Time Discrete Solver. Evaluating an expression at a previous time step that has not been stored results in an error.
|
The reaction force operator (reacf) evaluates the reaction force at each node point where a constraint is applied. The reaction force at a node is equal to the corresponding component of the negated residual vector −L computed while solving the model. The reaction forces are stored together with the solution vector by the solvers.
|
•
|
The reaction force operator (reacf) is useful when calculating integrals of reaction forces or fluxes.
|
|
•
|
Apply the reacf operator on the names of dependent variables when doing a surface integration. For example, in structural mechanics, with dependent variables u and v corresponding to x- and y-displacements, use reacf(u) and reacf(v) to access integrals of the reaction forces in the x- and y-direction, respectively. The integration for the reaction force is a summation over the nodes, so the integration method must be summation rather than integration. The automatic integration method in the integrations available under Results>Derived Values detects the use of the reacf operation and then uses the summation method.
|
|
•
|
Storing of the reaction forces can be disabled by clearing the Reaction forces check box in the Output section in the solver’s Settings window. This saves some computational time and memory. It is then not possible to use the reaction force operator.
|
|
•
|
You can call reacf with an optional second argument. The second argument is the dimension of the entity where the reaction force should be evaluated. The dimension is assumed to be at least equal to the dimension from where the call to reacf is made. This is different from reacf(u) only in the case when u is not defined on the entity where the operator is evaluated but only on adjacent entities of higher dimension.
|
|
•
|
It is also possible to call reacf with an optional third argument. This is a factor that the COMSOL Multiphysics software multiplies reacf(u,dim) by. The third argument is evaluated on each adjacent entity of dimension dim and multiplied by the reaction forces on that entity.
|
|
•
|
|
•
|
The expression realdot(a,b) treats complex numbers a and b as if they were real-valued vectors of length 2 and returns their dot product. Also think of the operator call as a shorthand form of real(a*conj(b)). This expression, however, is not an analytical function of its complex arguments and therefore has no unique partial derivatives with respect to a and b.
|
|
•
|
The difference between realdot(a,b) and real(a*conj(b)) is that the partial derivatives of the former with respect to a and b are defined as conj(b) and conj(a), respectively, while for the latter expression, the partial derivatives are real(conj(a)) and real(a).
|
 |
|
•
|
Common objective function quantities like power and energy must be redefined in terms of realdot(a,b) rather than real(a*conj(b)) for the sensitivity solver to compute correct derivatives. This applies also to the absolute value, abs(a), via the definition |a|2 = realdot(a, a).
|
|
•
|
To access the latest assembled residual, use the residual operator. For example, you can plot residual(spf.U) to get a plot of the latest residual of the velocity U in a fluid-flow simulation. The residual can provide insight into convergence issues by showing the locations where the algebraic residual is large.
|
|
•
|
To make the residual available in the simulation output (for plotting, for example), specify that the solver stores it both while solving and in the output by selecting While solving and in output from the Store last residual list in the Advanced solver node’s Settings window.
|
|
•
|
When the forward sensitivity operator (sens operator) is applied to an expression, COMSOL Multiphysics uses the forward sensitivity solution with respect to the indicated control variable instead of the primal solution for the evaluation. This means, in practice, that when the first argument is a linear expression in the dependent variables, the operator returns its derivative with respect to the control variable given as second argument. The result for a nonlinear expression usually lacks meaning.
|
|
•
|
For scalar control variables, access the corresponding forward sensitivity solution by giving the control variable name as the second argument to this operator. For example, with the dependent variable u and the scalar control parameter q, access the forward sensitivity solution ∂u/∂q as sens(u,q).
|
Use the operator setconst to define temporary constants while the second argument of the withsol operator (see withsol) is evaluated. For example, withsol('sol1',expr,setconst(a,3)) defines the variable a to have the value 3 while expr is evaluated. The setconst operator can be combined with setind or setval (see below) and does not affect the solution that is selected for evaluation.
You can use setconst with more than two arguments to make the syntax more compact. For example, withsol('sol1',expr,setconst(a,3,b,4)) is equivalent to withsol('sol1',expr,setconst(a,3),setconst(b,4)).
Use setind to specify a parameter index and setval to specify a parameter value in connection with the withsol operator (see withsol). For parametric sweeps over several parameters, say p and q, setval and setind can be used in any combination for the two parameters — for example, withsol('sol1',expr,setind(p,2,q,3)) or withsol('sol1',expr,setind(p,2),setval(q,5)).
Negative indices in setind are counted from the end. For example, in a time-dependent solver, withsol('sol1',expr,setind(t,-2)) evaluates expr at the second last time step. An alternative notation for the first and last indices is setind(p,'first') and setind(p,'last').
You can use setind and setval with more than two arguments to make the syntax more compact. For example, withsol('sol1',expr,setval(p,1,q,2)) is equivalent to withsol('sol1',expr,setval(p,1),setval(q,2)).
|
•
|
|
•
|
The argument u must be a dependent variable or a partial derivative of a dependent variable. In the latter case, the order returned is the order of the dependent variable itself and not the order of its derivative.
|
|
•
|
It is an error to apply the shapeorder operator to, for example, an expression, a constant, or a spatial coordinate.
|
|
•
|
The side operator can be called on an entity that has lower dimension than the model. The dimension of the entity from where the call is made is called n.
|
|
•
|
The side operator is an operator that evaluates an expression, not on the entity where it is called but instead on one of the adjacent entities of dimension n+1. You choose which entity by giving its number (this is the number displayed, for instance, in the selection fields) as the first argument to the operator.
|
|
•
|
It can happen that the entity you choose is adjacent to the evaluation point more than once. For instance, a boundary can have the same domain on both sides. In such cases the side operator takes the average of the different values.
|
|
•
|
The scope.ati(<coordinate expressions>, expr) operator evaluates the expression expr in the geometry with the given scope (typically comp1 for Component 1 or a similar scope for another Component branch) on an i-dimensional entity in the point given by the coordinate expressions (at0 for a 0-dimensional entity, at1 for a 1-dimensional entity, at2 for a 2-dimensional entity, and at3 for a 3-dimensional entity). For example, comp1.at1(0,y,dom) evaluates dom in the two-dimensional geometry on an edge in the point (0, y). To use a certain ati operator variant, there must be a geometric entity of the right dimension at the coordinates where it is evaluated; for example, at0 only works if the source geometry has a vertex in the point where you want to evaluate the expression. The number of arguments for the scope.ati operator is equal to the space dimension in the source component (the coordinate expressions) plus one (the expression to evaluate).
|
|
•
|
|
•
|
The subst operator takes a variable or expression as its first argument, followed by one or more argument pairs, each consisting of a variable name and an expression. The first argument in each pair is an original variable that appears in the variable or expression that you specify as the first argument, and the second argument in each pair is the variable or expression that you want to substitute the original variable with. This can be useful, for example, for replacing the variable for temperature in a temperature-dependent expression for some quantity by a fixed initial temperature for use as an initial condition.
|
|
•
|
As an example, the expression subst(hmnf.nutildeinit,p,pin_stat) (taken from the Sajben Diffuser model in the CFD Module Applications Libraries) substitutes the dependent variable for pressure, p, with a user-defined variable pin_stat for the inlet static pressure. The evaluation of the variable hmnf.nutildeinit (for the undamped turbulent kinematic viscosity) then takes the value of pin_stat instead of p.
|
|
•
|
The unit of the output from the subst operator is the same as the unit for its first input argument.
|
The sum operator, when used as sum(expr, index, lower, upper), is a summation operator that computes the sum of the terms expr for all index values from lower to upper. The expressions for lower and upper limits are required to evaluate to real values and to be independent of the evaluation point. For example, sum(i^2,i,1,4) = 12+22+32+42 = 30.
|
•
|
The test operator is available for modeling using the weak formulation of the equations.
|
|
•
|
This operator creates the test function for the variable that it operates on. For example, write ux*test(u) to represent ux times test function of u.
|
|
•
|
The timeint and timeavg operators integrate and compute the average of a time-dependent expression over a time interval, respectively. timeint(t1,t2,expr) and timeavg(t1,t2,expr)compute the integral and average of expr over the interval t=t1 to t=t2, respectively. The first two arguments must be real scalars. The integral is computed by numerical integration, subdividing the interval until the required accuracy is reached. The timeavg operator numerically integrates the expression in the same way as timeint and then divides the result by t2-t1.
|
|
•
|
timeint(t1,t2,expr,tol) and timeavg(t1,t2,expr,tol) set the relative tolerance in the numerical integration procedure to tol. The tolerance must be a positive real constant. The default tolerance (used when the fourth argument is omitted) is 1e-8.
|
|
•
|
timeint(t1,t2,expr,tol,minlen) and timeavg(t1,t2,expr,tol,minlen) set the smallest length of the subintervals used in numerical integration as a fraction of the length of the whole integration interval. Subintervals smaller than this length are not further subdivided even if that means that the required accuracy is not reached. minlen must be a positive real constant. The default value of minlen (used when the last argument is omitted) is 1e-4.
|
|
•
|
timeint(t1,t2,expr,'nointerp') and timeavg(t1,t2,expr,'nointerp') evaluate the time integral without doing any interpolation between the stored time steps. This variant might be less accurate but faster and more robust.
|
|
•
|
The timeint and timeavg operators can only be used during results evaluation, so you cannot use them when setting up the model.
|
|
•
|
The timemax and timemin operators evaluate the maximum and minimum, respectively, of an expression over time. timemax(t1,t2,expr) finds the maximum of expr on the interval t1 ≤ t ≤ t2. The first two arguments must be real constants.
|
|
•
|
timemax(t1,t2,expr,'nointerp') and timemin(t1,t2,expr,'nointerp') evaluate the maximum or minimum without doing any interpolation between the stored time steps. This variant might be less accurate but faster and more robust.
|
|
•
|
The timemax and timemin operators can only be used during results evaluation, so you cannot use then when setting up the model. See attimemax and attimemin for similar operators.
|
When deciding if a linear solver can be used, the treatasconst(expr) operator treats expr as independent of the solution (even if this is actually not the case).
|
•
|
The try_catch(tryExpr,catchExpr) operator attempts to evaluate the expression tryExpr, but if this fails for any point, the operator evaluates catchExpr instead.
|
|
•
|
Consider using the if operator (see if) with a suitable condition as the first argument instead of the try_catch operator, if the if operator is applicable.
|
|
•
|
COMSOL can evaluate expressions on both sides of a boundary. One way to do this is by using the up and down operators. These operators are available only on boundaries (that is, geometric entities of dimension one less then the dimension of the model).
|
|
•
|
Use the up and down operators to evaluate an expression on the upside or downside of the boundary. If the upside or downside is outside of the geometry, or if the variables in the expression are not active on that side, the up or down operator returns 0.
|
For more information about the upside and downside of a boundary, see Tangent and Normal Variables. See also side and mean for similar operators.
|
•
|
The var operator (variation operator) is available for modeling using the weak formulation of the equations.
|
|
•
|
The var operator has the same function as the test operator but is limited to the specified set of fields.
|
|
•
|
This operator creates the test function for the variable that it operates on. For an expression, such as var(F(u, ∇u, v, ∇v), a), where the dependent variable u is in the field named a and the dependent variable v is not, the var operator is equivalent to:
|
|
•
|
The with operator can access specific solutions during results evaluation.
|
|
•
|
Use the solution number as the first input argument. The second input argument is the expression that you want to evaluate using this solution. For example, with(3,u^2) provides the square of the third eigensolution for an eigenvalue problem.
|
|
•
|
You can also use 'first' or 'last' as the first argument to evaluate an expression at the first or last time of the simulation, respectively.
|
|
•
|
For example, you can use the with operator to verify that two eigensolutions are orthogonal or to compare two solutions at different time steps or parameter values.
|
|
•
|
If you want to use the with operator for a parametric problem, you should use a Parametric solver instead of a Parametric Sweep.
|
|
•
|
The with operator can only be used during results evaluation, so you cannot use it when setting up the model.
|
The withsol operator can access the solution from any solver sequence in the current model. It can be used as soon as the solution has been computed. The first argument is the tag of the solver sequence, and the second argument is an expression to evaluate using that solution. Additional arguments can be added to specify the time step, eigenvalue, or parameter value. See also setind and setval.
The withsol operator is similar to the with and at operators but is more general because it can access any solution in the current model.
|
•
|
|
•
|
For a time-dependent solver, withsol('sol1',expr) evaluates at the last stored time step in the solution. Other time steps can be specified by using the setind or setval operators as additional arguments. For example, withsol('sol1',expr,setval(t,0.5)) evaluates at the time step t = 0.5 (using interpolation between stored time steps if necessary), and withsol('sol1',expr,setind(t,3)) evaluates at the third stored time step.
|
|
•
|
For an eigenvalue solver, withsol('sol1',expr) evaluates at the first eigenvalue. Other eigenvalues can be specified using the setind operator as an additional argument. For example, withsol('sol1',expr,setind(lambda,2)) evaluates at the second eigenvalue. (The setval operator can also be used with eigenvalues, but this is not very useful because the exact eigenvalues must then be known.)
|
|
•
|
For a parametric sweep over a parameter p, withsol('sol1', expr) evaluates at the last parameter value. You can specify other parameter values using the setind or setval operators as additional arguments. For example, withsol('sol1',expr,setval(p,4)) evaluates with the parameter value p = 4. withsol('sol1',expr,setind(p,2)) evaluates for the second value of parameter p.
|
|
•
|