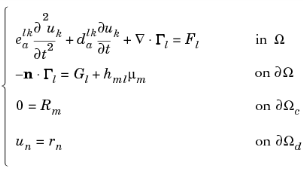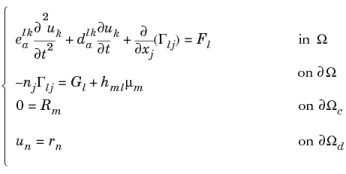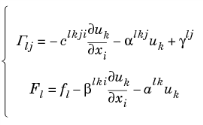All PDE interfaces and equation forms support multiple dependent variables. In the case of several dependent variables u1, u2, …, uN, a general form system of equations takes the following form:
The equation index l and k ranges from 1 to N, while the general constraint index m ranges from 1 to Mc and the Dirichlet condition index n ranges from 1 to Md. The total number of constraints is therefore M = Mc+Md. This discussion uses the summation convention. Fl, Gl, Rm, and rn are scalars, whereas Γl is a spatial vector. The mass and damping coefficients ea and da are N-by-N matrices, while the constraint force Jacobian h is an M-by-N matrix. Note that there are several Lagrange multipliers: μ1, μ2,…, μM.
For a more compact form, let u be a vector with components uk, let Γ be a matrix with components Γlj, and so on. Then the system of equations takes on the same form as given in Equation 16-1 for a single dependent variable.
It is also possible to write the system entirely on component form, where Γlj are components of the vector Γl, and nj components of the normal vector n. Then the system of equations becomes:
The coefficient form of an equation system with N dependent variables u1, u2, …, uN can be easily obtained from the general form PDE shown in Equation using the substitutions:
Where index k and l run over dependent variables form 1 to N, while index i and j run over space dimensions from 1 to K. This means that for the case of a system of equations with N dependent variables in K space dimensions, the coefficients have the following sizes:
|
•
|
ea is an N-by-N matrix
|
|
•
|
da is an N-by-N matrix
|
|
•
|
c is an N-by-N-by-K-by-K four-dimensional array
|
|
•
|
α is an N-by-N-by-K three-dimensional array
|
|
•
|
β is an N-by-N-by-K three-dimensional array
|
|
•
|
a is an N-by-N matrix
|
|
•
|
f is an N-vector
|
|
•
|
g is an N-vector
|
|
•
|
q is an N-by-N matrix
|