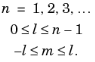Results

The solution provides a number of the lowest eigenvalues.

Three quantum numbers (n, l, m) characterize the eigenstates of a hydrogen atom:

•	n is the principal quantum number.

•	l is the angular quantum number.

•	m is the magnetic quantum number.

These quantum numbers are not independent but have the following mutual relationships:

An analytical expression exists for the energy eigenvalues in terms of the quantum number n

where

(4-4)

This expression is called the Bohr radius and has an approximate value of 3·10−11 m.

The first three energy eigenvalues, according to the above expression with μ ≈ me, are:

•	E1 ≈ –2.180·10−18 J

•	E2 ≈ –5.450·10−19 J

•	E3 ≈ –2.422·10−19 J

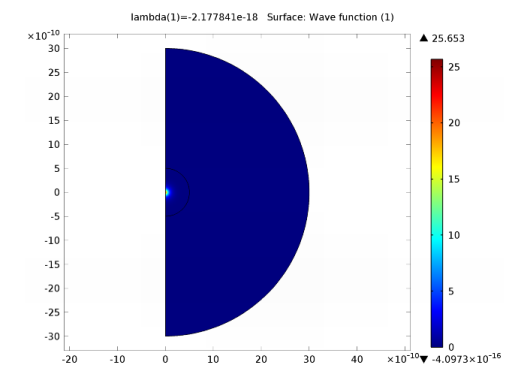
Figure 4-1: The wave function ψ for the first energy eigenvalue.

Comparing these numbers with the computed eigenvalues, you can see a 2-fold degeneracy for n = 2 and a 3-fold degeneracy for n = 3. This degeneracy corresponds to the following quantum triplets: (2,0,0) and (2,1,0); (3,0,0), (3,1,0), and (3,2,0). The computed values are separated due to the approximate numerical solution.

By refining the mesh and solving again, you can achieve more accurate results. The states with l = 0 correspond to spherically symmetric solutions, while states with l = 1 or 2 correspond to states with one or two radial node surfaces. The 0 energy level corresponds to the energy of a free electron no longer bounded to the nucleus. Energy levels closer to 0 correspond to excited states.

The wave function by itself has no direct physical interpretation. Another quantity to plot is ⏐Ψ⏐2, which is proportional to the probability density (unnormalized) function for the electron position after integration about the z-axis. The plot shows the unnormalized probability density function.

To determine the ground state energy, you can use adaptive mesh refinement.