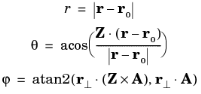Use a Spherical System (
) to define a spherical coordinate system in 3D by its origin, zenith axis, and azimuth axis.
) to define a spherical coordinate system in 3D by its origin, zenith axis, and azimuth axis.The coordinates of a local spherical coordinate system are (r, θ,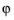 
), where r represents the radial distance from the origin, θ is the inclination (in the interval from 0 to π), and 
is the azimuthal angle (in the interval from −π to π). Specify—in terms of the global Cartesian coordinates x, y, and z—the position of the origin, the axis θ = 0 (the zenith axis, Z), and the axis θ = π/2, 
= 0 (the azimuth axis, A). The direction vectors are automatically normalized.
), where r represents the radial distance from the origin, θ is the inclination (in the interval from 0 to π), and 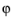is the azimuthal angle (in the interval from −π to π). Specify—in terms of the global Cartesian coordinates x, y, and z—the position of the origin, the axis θ = 0 (the zenith axis, Z), and the axis θ = π/2, 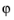= 0 (the azimuth axis, A). The direction vectors are automatically normalized.
where ro is the position of the origin, Z is a unit vector along the axis θ = 0, and the component of r − ro in the plane θ = π/2 is
In the Coordinate names table, the default Coordinate names are entered—r, theta, and phi. The labels for each coordinate name—First, Second, and Third—include the default name in parentheses.
Enter the location of the Origin in the global Cartesian coordinate system. The default is an origin coinciding with that of the global system.
Enter the Direction of axis θ=0 (the zenith axis). The default axis direction is the z direction in the global Cartesian system.
Define the Direction of axis θ=π/2, 
=0 (the azimuth axis). The default direction is the x direction in the global Cartesian system.
=0 (the azimuth axis). The default direction is the x direction in the global Cartesian system.
 |
Go to Name for information about the Settings window Label and Name. Also see Settings and Properties Windows for Features Nodes.
|