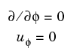General Single-Phase Flow Theory

The Single-Phase Fluid Flow interfaces are based on the Navier-Stokes equations, which in their most general form read

(13-1)

(13-2)

(13-3)

where

•	ρ is the density (SI unit: kg/m3)

•	u is the velocity vector (SI unit: m/s)

•	p is pressure (SI unit: Pa)

•	τ is the viscous stress tensor (SI unit: Pa)

•	F is the volume force vector (SI unit: N/m3)

•	Cp is the specific heat capacity at constant pressure (SI unit: J/(kg·K))

•	T is the absolute temperature (SI unit: K)

•	q is the heat flux vector (SI unit: W/m2)

•	Q contains the heat sources (SI unit: W/m3)

•	S is the strain-rate tensor:

The operation “:” denotes a contraction between tensors defined by

(13-4)

This is sometimes referred to as the double dot product.

Equation 13-1 is the continuity equation and represents conservation of mass. Equation 13-2 is a vector equation which represents conservation of momentum. Equation 13-3 describes the conservation of energy, formulated in terms of temperature. This is an intuitive formulation that facilitates boundary condition specifications.

To close the equation system, Equation 13-1 through Equation 13-3, constitutive relations are needed. For a Newtonian fluid, which has a linear relationship between stress and strain, Stokes (Ref. 1) deduced the following expression:

(13-5)

The dynamic viscosity, μ (SI unit: Pa·s), for a Newtonian fluid is allowed to depend on the thermodynamic state but not on the velocity field. All gases and many liquids can be considered Newtonian. Examples of non-Newtonian fluids are honey, mud, blood, liquid metals, and most polymer solutions.

When you have the CFD Module or the Microfluidics Module, you can model flows of non-Newtonian fluids using the predefined power law and Carreau models, which describe the dynamic viscosity for non-Newtonian fluids.

Other commonly used constitutive relations are Fourier’s law of heat conduction and the ideal gas law.

In theory, the same equations describe both laminar and turbulent flows. In practice, however, the mesh resolution required to simulate turbulence with the Laminar Flow interface makes such an approach impractical.

There are several books where derivations of the Navier-Stokes equations and detailed explanations of concepts such as Newtonian fluids can be found. See, for example, the classical text by Batchelor (Ref. 3) and the more recent work by Panton (Ref. 4).

Many applications describe isothermal flows for which Equation 13-3 is decoupled from Equation 13-1 and Equation 13-2.

2D Axisymmetric Formulations

A 2D axisymmetric formulation of Equation 13-1 and Equation 13-2 requires to be zero. That is, there must be no gradients in the azimuthal direction. A common additional assumption is however that uφ=0. In such cases, the 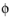-equation can be removed from Equation 13-2. The resulting system of equations is both easier to converge and computationally less expensive compared to retaining the 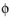-equation. The default 2D axisymmetric formulation of Equation 13-1 and Equation 13-2 therefore assumes that